Algoritmos Complejos

Bitácora Inicial: Durante esta semana trabajamos en algoritmos un tanto complejos que consistían en encontrar los números primos de n números dados.
Los números primos son aquellos que solo resultan divisibles por sí mismos y por la unidad. Los que pueden dividirse por otros números, se denominan compuestos (por ejemplo el 9 que además de dividirse por 9 y por 1, también puede dividirse exactamente por 3). Fueron ya conocidos en la antigüedad por la civilización griega, habiendo sido usados por Euclides, quien demostró que poseen la particularidad de ser infintos.

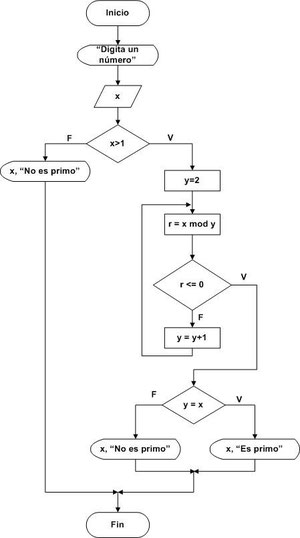
Este es el pseudocodigo:

Inicio
 Definir indice, temp como Entero
 Escribir "Numeros: 1,2"
 Indice = 3
Temp = 2
  Sí indice < 3 entonces
    temp=2
    Sí temp < indice %2 entonces
      Sí (Indice%2) y (temp=0) entonces
      Escribir "No es un numero primo"
       temp=++
    sino
      Escribir "Es un numero primo"
Fin

De igual forma realizamos un algoritmo para determinar una serie de numeros finobacci, y el cual consistio en lo siguiente.
Se llaman números de Fibonacci a aquellos que forman parte de la sucesión infinita de números naturales donde cada número se calcula sumando los dos anteriores a él.
La sucesión de Fibonacci es la siguiente sucesión de números enteros positivos:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

La sucesión de Fibonacci se puede escribir como una "regla": la regla es xn = xn-1 + xn-2 donde: xn es el término en posición "n" xn-1 es el término anterior (n-1) xn-2 es el anterior a ese (n-2) Por ejemplo el sexto término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8.

#include <iostream.h>

#include <conio.h>

int main()

{   int x, cont=0, P=0, F=1, S;

    cout<< "digita el valor de x: ";

    cin>> x;

    do

    { cout<< P <<" ";

    S=P+F;

    P=F;

    F=S;

    cont++ ;

    } while(cont < x);

    getch();

    return 0;

}